The science behind the legends I: Was Heron's crown made of gold?

Within the popular culture related to science and scientists, a prominent place is occupied by three legends. In the first one, Archimedes runs naked shouting Eureka!, in the second one Galileo drops two bodies of different weights from the Leaning Tower of Pisa and in the third one, an apple hits Newton's head who was enjoying his nap under a tree.

All three are often recounted in textbooks even though they have no historical basis. Unfortunately, students are not offered more than anecdotal, and they are not used to their advantage in understanding physics.

To provide an opportunity to learn about authentic scientific reasoning, the article series entitled The Science Behind the Legends offers a discussion of the scientific knowledge behind these famous tales.

Was Heron's crown made of gold?

Archimedes (287-212? BC) was a Greek mathematician, physicist, and engineer. In mathematics, he made the first precise calculation of the quotient between the circumference and the diameter of a circle and invented the method of calculating volumes and areas of geometric bodies such as spheres and cylinders.

In physics, his most important contribution was the quantification of the thrust force, known today as "Archimedes' principle": the magnitude of the thrust force on a body, partially or immersed in a fluid, is equal to the weight of the fluid displaced by the body. In engineering, he contributed a large number of inventions, from "Archimedes' screw" to the catapult.

Many legends are told about Archimedes, which shows that his work provoked public attention and aroused the imagination of his admirers. It was said that he was able to ignite the Roman fleet using a system of mirrors or that he cared more about the calculations he made in the sand than the mortal danger he was in after the conquest of Syracuse by Roman soldiers. But the most famous legend is undoubtedly the one that tells how Archimedes solved the problem that King Heron had with his new crown, supposedly made of gold.

Two current ways of narrating the legend

The origin of the legend is related to the amazement of the people at the fact that it was possible to determine the composition of a crown without damaging or melting it, i.e. the initial impulse to create it was the popular appreciation of the solution of the problem based on brilliant scientific reasoning. The place of the discovery (a public bath) or the manner of announcing the solution (running naked and shouting Eureka!) were probably "narrative embellishments" to make the story more attractive to listeners.

Now, after more than twenty centuries have passed, it is no miracle that the legend is narrated for other purposes. For those for whom science is no longer miraculous, but very dangerous, the problem and the solution are less important than the negative image of scientists that can be projected to society by falsifying the legend.

The scientist who, upon finding the solution, has no shame and runs naked through the streets is a useful archetype of someone prone to sell his soul to the devil to advance his scientific work. If the legend is told for such a purpose, then the essentials of the original situation (the problem and the solution) are lost and everything is reduced to "narrative embellishments" that implicitly carry a message against science and scientists.

Another way to distort the legend is to attribute to Archimedes a method of solving the problem that was certainly not used by him. In physics textbooks, it is suggested that Archimedes measured the weight of the crown in air and its apparent weight when immersed in water. Knowing the weight of the crown in air and the weight loss due to buoyancy, Archimedes was supposedly able to calculate the density of the crown and, by comparing it with the density of pure gold, was in a position to tell whether the crown was pure gold or not. Since Archimedes did not know the numerical value of the densities of gold and water and did not have the present formulas for calculating the density of the crown with the above data, this method of solving the problem could not have been his.

How did Archimedes solve the crown problem? The answer to this question is not known with certainty, but it is possible to reflect on possible avenues of solution consistent with the state of knowledge of physics and mathematics at the time of Archimedes.

The Heron's crown problem

Everyone knows that King Heron wanted to have a new crown and that he gave his silversmith a known quantity of pure gold to make it. Upon receiving the crown, which weighted the gold delivered, the king wanted to know if the crown was indeed pure gold or if the silversmith replaced some of the gold with silver.

The "strong formulation" of the problem would be: Assuming the crown was made of gold and silver, what was the percentage of silver? Understanding the possible solutions of such a formulation requires quite advanced physical reasoning and mathematical procedures and, therefore, "the strong formulation" would be suitable for high school or first-year college physics students.

It should be noted that the best-known version of the legend, published by the Roman architect Marcus Vitruvius presents the problem in its "strong formulation" (what was the percentage of silver?). Interestingly, Vitruvius does not provide the details of the solution, i.e., it is left to the reader to figure out how to calculate the percentage of silver in the crown using volumes corresponding to the crown and to pieces of gold and silver whose masses are equal to the mass of the crown.

For high school students, the "weak formulation" of the crown problem would be more appropriate: Was the crown made of pure gold?

It is very important to insist that the crown delivered weighed the same as the gold received by the silversmith, because some students believe that the crown weighed less and that the king, upon receiving it, could not notice it because there were no scales. For them, Archimedes' procedure was a complicated way to measure the weight of the crown. Therefore, in formulating the problem, it is of utmost importance to clarify this point. Perhaps, by narrating the corresponding part of the legend like this:

The king took two pieces of pure gold, put them on the scales, and showed the silversmith that they were of the same weight. He also warned that, upon receiving the crown, he would compare its weight with the weight of the masterpiece that would remain in his possession. When the silversmith delivered the crown, the king did as he had been warned, compared the weights of the crown and the masterpiece with the scales, and found that the crown did indeed have the expected weight.

Each narrator can add the details that explain why the king's distrust arises (e.g., his advisor whispered something to him or a rumor spread that the silversmith wanted to show his fiancée that he was clever enough to steal the royal gold without the king noticing). What matters is to formulate the problem more simply: Was the crown made of pure gold or not?

It is also useful to add the "real" conditions for finding the solution. First, the crown cannot, in any way, be damaged. Second, the king, due to his mathematical ignorance, did not want to accept any calculation as part of the solution. That is to say, the procedure should be so simple and so conclusive that there should not be the slightest doubt about the composition of the crown.

Possible Archimedean solutions

How was Archimedes solve the problem while respecting the actual conditions? Archimedes has the crown and a piece of gold of the same mass and must discover, without even scratching the crown, whether it is made of pure gold.

If the crown and the piece of gold are made of the same substance, then they must have the same density. That is, apart from the same mass, they must have the same volume. Thus, the problem of the crown is reduced to a more specific problem: how to compare the volumes of two bodies, at least one of which (the crown) has an irregular shape whose volume cannot be calculated?

Comparing volumes through dislodged water

If a body is immersed in a container with water, the water level in the container rises. This is due to the displacement of water by the presence of the body (the water cannot occupy the space occupied by the body). The volume of water displaced is equal to the volume of the submerged body. Archimedes was able to use this fact to compare the volumes of the standard piece and the crown.

A glass container with water is required for the demonstration. The size should be adequate. If it is too large it will not be possible to notice small differences in water levels. If it is too small, the water will run out and, again, comparison of volumes will be impossible.

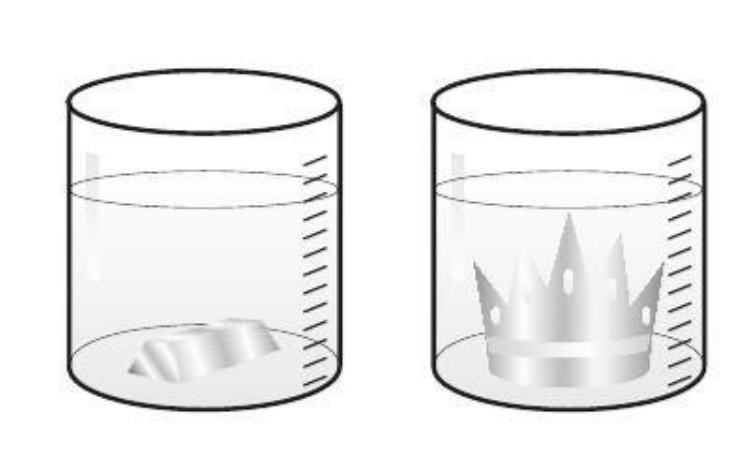
Archimedes was able to put the standard piece in and mark the new water level in the vessel because of its presence. After removing the standard piece, the crown is put on. Before putting it on, Archimedes was able to explain to the king:

If the crown is made of pure gold, its volume is equal to the volume of the pattern piece, and the water level, with the crown submerged, will be the same. If in the construction of the crown some gold was replaced by silver, the volume of the crown will be greater than the volume of the standard piece. This is because the density of silver is less than the density of gold. If the amount of silver added has the same mass as the missing gold, it must have a larger volume. If this is the case, the water level, with the crown submerged, should be higher.

Although conceptually very transparent, this possible solution received a lot of criticism, even Galileo Galilei criticized it for possible inaccuracies. Therefore, it would be good to discuss with the students what factors could cause errors when measuring the volumes of the standard piece and the crown and estimate the value of the possible error in cubic millimeters. For example, for a cylindrical vessel whose radius is 150 millimeters, an error in the level marking of a single hundredth of a millimeter leads to an error in the volume comparison that is greater than 700 cubic millimeters.

To elaborate further on this idea, a good question might be: Of two cylindrical containers of the same capacity but one taller than the other, which would be more suitable for comparing volumes?

Comparing volumes through thrust force

If Archimedes realized that the first method is not accurate enough, he could use the thrust force to compare volumes indirectly with much greater accuracy. His explanation to the king may have been this:

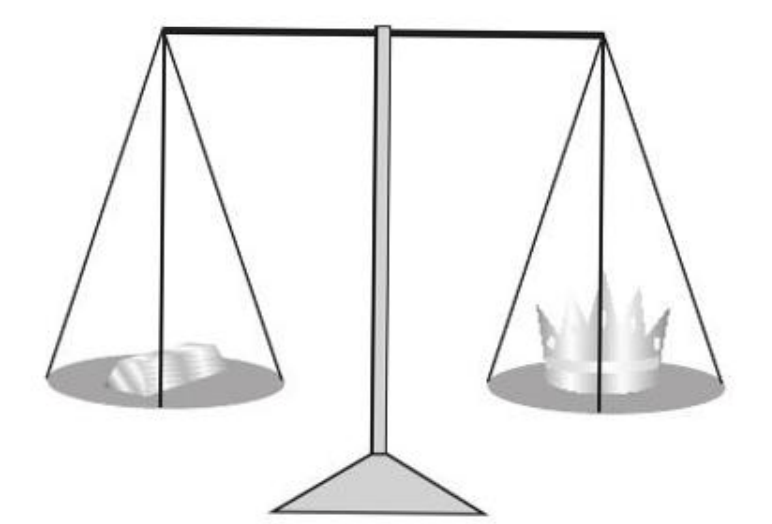
The crown and the standard piece have the same weight, which was shown using the balance. If the crown is made of pure gold, it has the same volume as the standard piece. Since they have the same volume, both, when immersed in water, will dislodge the same amount of water and suffer the same buoyancy force (equal, as I have just shown, to the weight of water dislodged). In such a case, the balance of the balance will not be affected by immersing the crown and the standard piece in water.

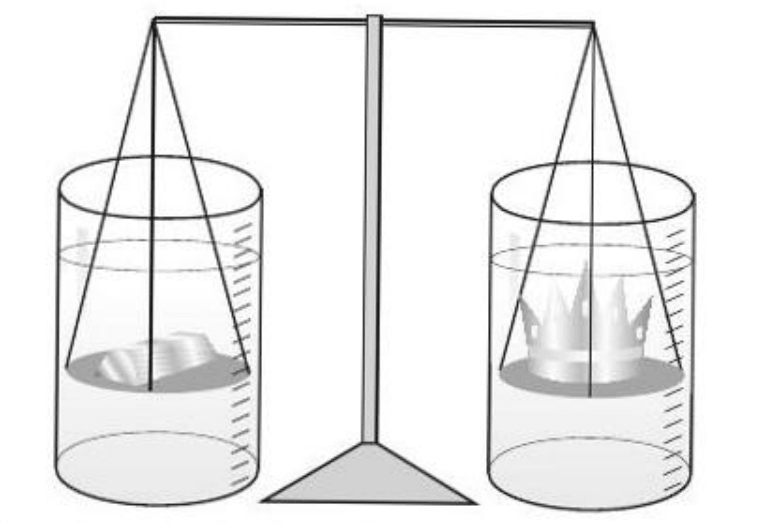
If some gold is missing from the crown and the missing mass is "made up" by adding silver, the volume of the crown will be greater than the volume of the standard piece. This is because the density of silver is less than the density of gold. If the amount of silver added has the same mass as the missing gold, it must have a larger volume. If this is the case, the submerged crown will suffer a greater thrust force and, by submerging the crown and the standard piece, the balance of the balance will not be maintained. The apparent weight of the standard piece will be greater and the end from which it is hanging will drop.

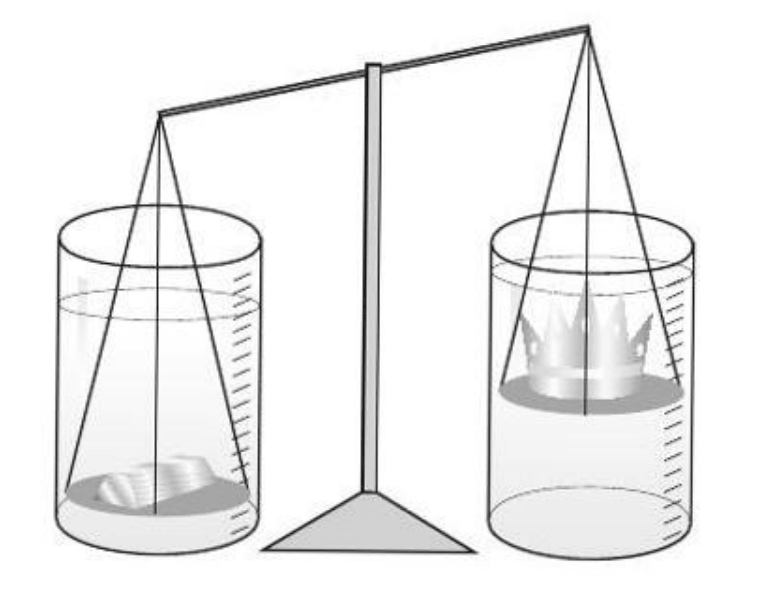
To demonstrate to the students the great difference in precision between these two methods of comparing volumes, it would be good to have a sensitive balance. When establishing equilibrium between a body and the corresponding weights, explore with the students how many drops of water, placed with an eyedropper on one of the pans, are enough to unbalance the balance. Usually, it is only a few. Their volume (a few cubic millimeters) represents the possible error in comparing volumes indirectly using the buoyancy force.

In conclusion

How the legend ends, with an honest or dishonest silversmith, depends on the personal taste of the narrator. Whatever the fate of the silversmith, it is certain that students, with the approach outlined above, will have full experience with the reasoning underlying the two different paths to the solution of a famous problem in the history of science. Moreover, students will see that these paths are not equivalent concerning the certainty of the conclusions, since in one the possible errors are greater than in the other. Knowing the limits of science is as important as admiring its intellectual beauty.

Author: Josip Slisko, Source: Correo del Maestro. No. 29, p.23-36.